9.8 KiB
9.8 KiB
Features
Features analysis
# Calculate different percentiles
percentiles = [1, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95, 99]
print("\nPercentiles:")
for p in percentiles:
print(f"{p}th percentile: {df['target'].quantile(p/100):.6f}")
# Plot distribution
plt.figure(figsize=(15, 10))
# Plot 1: Overall distribution
plt.subplot(2, 2, 1)
sns.histplot(df['target'], bins=100)
plt.title('Distribution of Returns')
plt.axvline(x=0, color='r', linestyle='--', alpha=0.5)
# Plot 2: Distribution with potential thresholds
plt.subplot(2, 2, 2)
sns.histplot(df['target'], bins=100)
plt.title('Distribution with Potential Thresholds')
# Add lines for different standard deviations
std = df['target'].std()
mean = df['target'].mean()
for i in [0.5, 1.0, 1.5]:
plt.axvline(x=mean + i*std, color='g', linestyle='--', alpha=0.3, label=f'+{i} std')
plt.axvline(x=mean - i*std, color='r', linestyle='--', alpha=0.3, label=f'-{i} std')
plt.legend()
# Let's try different threshold approaches
# Approach 1: Standard deviation based
std_multiplier = 0.2
std_threshold = std_multiplier * std
labels_std = np.where(df['target'] > std_threshold, 1,
np.where(df['target'] < -std_threshold, -1, 0))
# Approach 2: Percentile based
percentile_threshold = 0.2 # top/bottom 20%
top_threshold = df['target'].quantile(1 - percentile_threshold)
bottom_threshold = df['target'].quantile(percentile_threshold)
labels_percentile = np.where(df['target'] > top_threshold, 1,
np.where(df['target'] < bottom_threshold, -1, 0))
# Plot 3: Distribution of STD-based classes
plt.subplot(2, 2, 3)
sns.histplot(data=pd.DataFrame({'return': df['target'], 'class': labels_std}),
x='return', hue='class', bins=100)
plt.title(f'Classes Based on {std_multiplier} Standard Deviation')
plt.axvline(x=std_threshold, color='g', linestyle='--', alpha=0.5)
plt.axvline(x=-std_threshold, color='r', linestyle='--', alpha=0.5)
# Plot 4: Distribution of Percentile-based classes
plt.subplot(2, 2, 4)
sns.histplot(data=pd.DataFrame({'return': df['target'], 'class': labels_percentile}),
x='return', hue='class', bins=100)
plt.title(f'Classes Based on {percentile_threshold*100}th Percentiles')
plt.axvline(x=top_threshold, color='g', linestyle='--', alpha=0.5)
plt.axvline(x=bottom_threshold, color='r', linestyle='--', alpha=0.5)
plt.tight_layout()
plt.show()
# Print class distributions
print("\nClass Distribution (STD-based):")
print(pd.Series(labels_std).value_counts(normalize=True))
print("\nClass Distribution (Percentile-based):")
print(pd.Series(labels_percentile).value_counts(normalize=True))
# Calculate mean return for each class
print("\nMean Return by Class (STD-based):")
std_df = pd.DataFrame({'return': df['target'], 'class': labels_std})
print(std_df.groupby('class')['return'].mean())
print("\nMean Return by Class (Percentile-based):")
perc_df = pd.DataFrame({'return': df['target'], 'class': labels_percentile})
print(perc_df.groupby('class')['return'].mean())
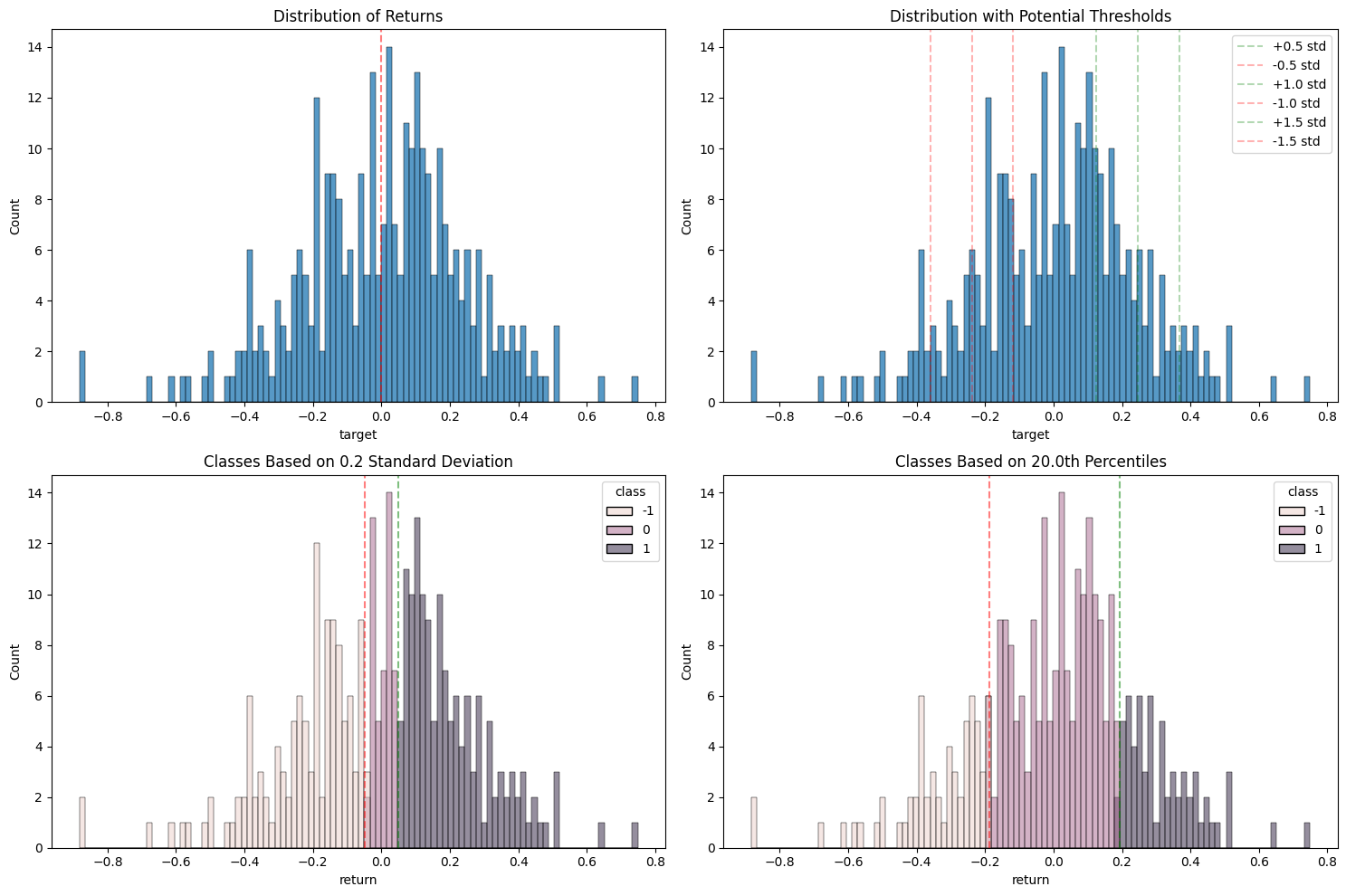
Target to classes
Based on std dev
# Read and prepare the data
df = pd.read_csv('model_data.csv')
df = df.drop('ts_event', axis=1)
# Separate features and target
X = df.drop('target', axis=1)
y = df['target']
# Split the data first so we only use train data statistics for thresholds
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Calculate threshold based on training data only
train_std = y_train.std()
threshold = 0.2 * train_std
# Transform targets into classes (update this function) instead of -1,0,1 do 0,1,2
def create_labels(y, threshold):
return np.where(y > threshold, 2,
np.where(y < -threshold, 0, 1))
y_train_classes = create_labels(y_train, threshold)
y_test_classes = create_labels(y_test, threshold)
# Print class distribution
print("Training Class Distribution:")
print(pd.Series(y_train_classes).value_counts(normalize=True))
print("\nTest Class Distribution:")
print(pd.Series(y_test_classes).value_counts(normalize=True))
based on percentile/threshold
Features importance
#XGB top 20 feature importance
feature_importance = pd.DataFrame({
'feature': X.columns,
'importance': xgb_model.feature_importances_
})
feature_importance = feature_importance.sort_values('importance', ascending=False).head(20)
plt.figure(figsize=(12, 6))
sns.barplot(x='importance', y='feature', data=feature_importance)
plt.title('Top 20 Most Important Features')
plt.xlabel('Feature Importance')
plt.tight_layout()
plt.show()
Features selection
Prediction
evaluation
# Calculate directional accuracy
directional_accuracy = (np.sign(y_pred) == np.sign(y_test)).mean()
print(f"Directional Accuracy: {directional_accuracy:.4f}")
#confusion matrix
from sklearn.metrics import confusion_matrix
# Plot confusion matrix
plt.figure(figsize=(10, 8))
cm = confusion_matrix(y_test_classes, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.title('Confusion Matrix')
plt.ylabel('True Label')
plt.xlabel('Predicted Label')
plt.show()
calculated returns based on various probability prediction thresholda
# .predict_proba() gives the probabilities for each class
print("Predicted probabilities:", model.predict_proba(X_test))
# Output example:
# [
# [0.35, 0.65], # 35% not spam, 65% spam
# [0.70, 0.30], # 70% not spam, 30% spam
# [0.45, 0.55], # 45% not spam, 55% spam
# ]
Chart probabilities
# Predict probabilities for each class
probabilities = model.predict_proba(X_test) # Shape: (n_samples, n_classes)
results_df = pd.DataFrame({
'Date': dates_test,
'Short Probability': probabilities[:, 0], # Probability of class 0 (short)
'Neutral Probability': probabilities[:, 1], # Probability of class 1 (neutral)
'Long Probability': probabilities[:, 2] # Probability of class 2 (long)
}).sort_values(by='Date') # Sort by date for time series plotting
fig = go.Figure()
# Add lines for each class probability
fig.add_trace(go.Scatter(
x=results_df['Date'], y=results_df['Short Probability'],
mode='lines', name='Short (Class 0)', line=dict(color='red')
))
fig.add_trace(go.Scatter(
x=results_df['Date'], y=results_df['Neutral Probability'],
mode='lines', name='Neutral (Class 1)', line=dict(color='orange')
))
fig.add_trace(go.Scatter(
x=results_df['Date'], y=results_df['Long Probability'],
mode='lines', name='Long (Class 2)', line=dict(color='green')
))
# Add title and labels
fig.update_layout(
title="Time Series of Predicted Class Probabilities",
xaxis_title="Date",
yaxis_title="Probability",
legend_title="Class"
)
fig.show()
cumulative returns bases od prob predictions
# Calculate returns based on probablity predictions
def calculate_returns(predictions, actual_returns, confidence_threshold=0.0):
pred_probs = final_model.predict_proba(X_test_selected)
max_probs = np.max(pred_probs, axis=1)
# Only take positions when confidence exceeds threshold
positions = np.zeros_like(predictions, dtype=float)
confident_mask = max_probs > confidence_threshold
# Convert predictions 0->-1, 2->1 for returns calculation
adj_predictions = np.where(predictions == 2, 1, np.where(predictions == 0, -1, 0))
positions[confident_mask] = adj_predictions[confident_mask]
returns = positions * actual_returns
return returns, np.mean(confident_mask)
# Test different confidence thresholds
confidence_thresholds = [0.4, 0.5, 0.6, 0.7, 0.8]
results = []
for conf_threshold in confidence_thresholds:
returns, coverage = calculate_returns(y_pred, y_test.values, conf_threshold)
# Calculate metrics
sharpe = np.sqrt(252) * returns.mean() / returns.std()
accuracy = accuracy_score(y_test_classes[returns != 0],
y_pred[returns != 0])
results.append({
'confidence_threshold': conf_threshold,
'sharpe': sharpe,
'accuracy': accuracy,
'coverage': coverage
})
##Plot difference confidence threshodls
# Plot cumulative returns
plt.figure(figsize=(12, 6))
for th in confidence_thresholds:
returns, _ = calculate_returns(y_pred, y_test.values, th) # Using 0.6 confidence threshold
cumulative_returns = (1 + returns).cumprod()
plt.plot(cumulative_returns)
plt.title('Cumulative Returns (0.6 confidence threshold)')
plt.xlabel('Trade Number')
plt.ylabel('Cumulative Return')
plt.grid(True)
plt.show()
results_df = pd.DataFrame(results)
print("\nPerformance at different confidence thresholds:")
print(results_df)
# Plot feature importance
importance_df = pd.DataFrame({
'feature': selected_features,
'importance': final_model.feature_importances_
})
importance_df = importance_df.sort_values('importance', ascending=False)
plt.figure(figsize=(12, 6))
sns.barplot(x='importance', y='feature', data=importance_df)
plt.title('Feature Importance')
plt.xlabel('Importance')
plt.tight_layout()
plt.show()
charts
# Actual vs predicted values
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, alpha=0.5)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
plt.xlabel('Actual Returns')
plt.ylabel('Predicted Returns')
plt.title('Actual vs Predicted Returns')
plt.tight_layout()
plt.show()